数学是理解世界的基础工具之一，其中整式作为数学中的基础构造，对于理解数学运算规则、解决实际问题具有重要意义，本文将围绕“整式”这一主题展开专题探讨，带领读者深入了解整式的概念、性质、运算及应用。

整式的概念

整式是由变量、常数以及加、减、乘、乘方运算构成的代数式，与分式不同，整式中不存在分母，整式是数学中非常基础且重要的一部分，对于解决代数问题、几何问题以及实际应用问题都具有重要作用。

整式的性质

整式具有许多重要的性质，这些性质为整式的运算和应用提供了基础，以下是一些主要的整式性质：

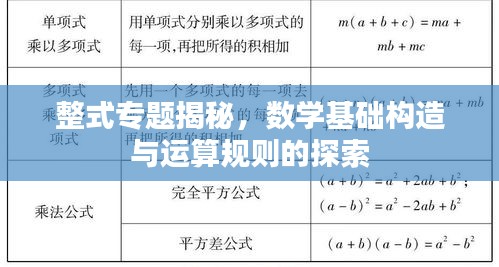
1、分配律：在整式中，乘法分配律是最基本的性质之一，它帮助我们简化复杂的整式运算。

2、幂的性质：包括乘方运算的基本规则，如(a^m)^n = a^(m*n)，(a*b)^n = a^n * b^n等。

3、因式分解：整式的因式分解是其另一个重要性质，它帮助我们简化整式，并揭示整式内部的结构。

整式的运算

整式的运算主要包括加法、减法、乘法、除法和乘方，乘法是整式运算的核心，通过乘法可以推导出其他运算规则，在整式的运算中，我们需要遵循代数的基本规则，如交换律、结合律等，还需要掌握一些特殊的运算技巧，如合并同类项、提取公因子等。

整式的应用

整式在各个领域都有广泛的应用，在代数领域，整式是解决代数方程的基础工具，在几何领域，整式用于表示图形的面积、体积等属性，在物理、工程、经济等领域，整式也发挥着重要作用，在物理中，整式用于描述物体的运动规律；在工程中，整式用于计算复杂的系统模型；在经济中，整式用于预测和规划经济发展趋势。

专题探讨

本文将针对一些典型的整式专题进行探讨，包括：因式分解的方法与技巧、整式的化简与求解、整式在几何中的应用等，通过专题探讨，我们将更深入地理解整式的内涵与外延，掌握解决整式问题的策略与方法。

整式作为数学中的基础构造，对于理解数学运算规则、解决实际问题具有重要意义，本文围绕整式的概念、性质、运算及应用展开专题探讨，希望通过本文的阐述，读者能对整式有更深入的理解，掌握解决整式问题的策略与方法，我们将继续关注整式的研究与应用，探索其在各个领域的发展潜力。

总结全文，本文详细介绍了整式的概念、性质、运算及应用，并针对一些典型的整式专题进行探讨，希望通过本文的阐述，读者能对整式有更深入的了解，为今后的数学学习与应用打下坚实的基础。