勾股定理是数学领域中的一颗璀璨明珠，其历史悠久，应用广泛，本文将围绕勾股定理的模型专题展开研究，探讨其内涵、应用及其在实际生活中的重要性。

勾股定理概述

勾股定理，又称毕达哥拉斯定理，是一个基本的几何定理，它描述了在直角三角形中，两条直角边的平方和等于斜边的平方，这一原理在数学、物理、工程等领域有着广泛的应用。

勾股定理模型专题

勾股定理的应用广泛且形式多样，以下将介绍几种典型的勾股定理模型专题。

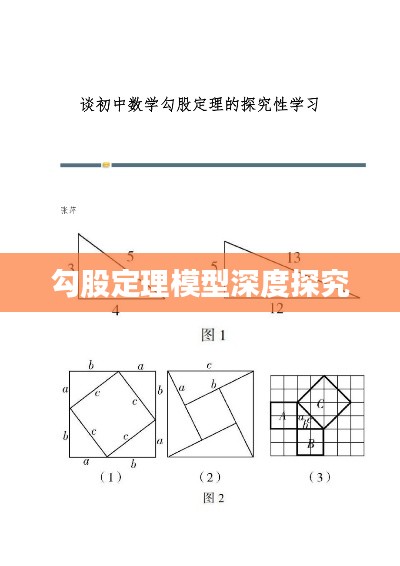
1、直角三角形模型：这是勾股定理最直接的应用，在求解与直角三角形相关的问题时，如三角形的边长、角度等，可以利用勾股定理进行求解。

2、梯形模型：在某些涉及梯形的问题中，可以通过构造辅助线，将梯形问题转化为与直角三角形相关的问题，进而应用勾股定理求解。

3、三角形与圆的结合模型：勾股定理在解决与圆相关的问题时也有广泛应用，在求解与圆内接三角形相关的问题时，可以利用勾股定理求解三角形的边长或角度。

4、动态图形模型：动态图形中的某些问题也可以通过构建勾股定理模型进行求解，这类问题通常涉及图形的运动变化，需要灵活运用几何知识进行分析。

勾股定理在实际生活中的应用

勾股定理不仅在数学、物理、工程等领域有广泛应用，还在实际生活中发挥着重要作用，在建筑领域，勾股定理被广泛应用于计算建筑物的层高、跨度等；在导航领域，勾股定理被用于计算航线距离；在计算机科学领域，勾股定理也被用于图像处理、计算机图形学等领域。

案例分析

为了更好地理解勾股定理模型专题，以下将通过具体案例进行分析。

案例一：求解直角三角形的边长，在一个直角三角形中，已知两条直角边的长度，求斜边的长度，可以通过勾股定理进行计算，即斜边的平方等于两直角边的平方和。

案例二：求解梯形的问题，通过将梯形问题转化为与直角三角形相关的问题，利用勾股定理求解，已知梯形的两腰和一条对角线，求另一条对角线的长度。

案例三：动态图形中的问题，在一个涉及图形运动变化的问题中，通过构建勾股定理模型进行求解，在一个动态图形中，两个线段在运动中始终保持垂直关系，求它们的长度变化关系。

勾股定理作为数学领域中的基本定理之一，其模型专题研究具有重要的理论价值和实践意义，本文介绍了勾股定理的概述、模型专题、实际应用及案例分析等方面内容，旨在帮助读者更好地理解和掌握勾股定理的相关知识，通过深入研究勾股定理模型专题，不仅可以提高数学素养和解决问题的能力，还可以为实际应用提供有力支持。